A monte carlo pin cell spectral code for nuclear engineering applications.
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Macros
Functions
vector.h File Reference

Utility functions for commonly used vector operations. More...

Go to the source code of this file.

Functions

template<typename T >
T dotProduct2D (T x1, T y1, T x2, T y2)
 Computes the dot product of two vectors in the 2D cartesian space. More...
 
template<typename T >
T dotProduct3D (T x1, T y1, T z1, T x2, T y2, T z2)
 Computes the dot product of two vectors in 3D cartesian space. More...
 
template<typename T >
T norm2D (T x, T y)
 Computes the norm of a vector in the 2D cartesian space. More...
 
template<typename T >
T norm3D (T x, T y, T z)
 Computes the norm of a vector in 3D cartesiance space. More...
 

Detailed Description

Utility functions for commonly used vector operations.

Author
William Boyd (wboyd.nosp@m.@mit.nosp@m..edu)
Date
April 14, 2013

Function Documentation

template<typename T >
T dotProduct2D ( T  x1,
T  y1,
T  x2,
T  y2 
)

Computes the dot product of two vectors in the 2D cartesian space.

This method computes the scalar product of two 2D vectors as follows: 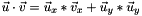$ \vec{u}\cdot\vec{v}=\vec{u}_x *\vec{v}_x + \vec{u}_y * \vec{u}_y $

Parameters
x1the x-coodinate of the first vector
y1the y-coordinate of the first vector
x2the x-coordinate of the second vector
y2the y-coordinate of the second vector
template<typename T >
T dotProduct3D ( T  x1,
T  y1,
T  z1,
T  x2,
T  y2,
T  z2 
)

Computes the dot product of two vectors in 3D cartesian space.

This method computes the scalar product of two 3D vectors as follows: 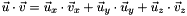$ \vec{u}\cdot\vec{v}=\vec{u}_x\cdot\vec{v}_x + \vec{u}_y\cdot\vec{u}_y + \vec{u}_z\cdot\vec{v}_z $

Parameters
x1the x-coodinate of the first vector
y1the y-coordinate of the first vector
z1the z-coordinate of the first vector
x2the x-coordinate of the second vector
y2the y-coordinate of the second vector
z2the z-coordinate of the second vector
template<typename T >
T norm2D ( T  x,
T  y 
)

Computes the norm of a vector in the 2D cartesian space.

This method computes the norm of a vector 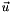$ \vec{u} $ in 2D as follows: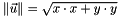 $ \| \vec{u} \| = \sqrt{x \cdot x + y \cdot y} $

Parameters
xthe x-coordinate of the vector
ythe y-coordinate of the vector
template<typename T >
T norm3D ( T  x,
T  y,
T  z 
)

Computes the norm of a vector in 3D cartesiance space.

This method computes the norm of a vector 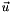$ \vec{u} $ in 3D as follows: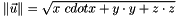 $ \| \vec{u} \| = \sqrt{x\ cdot x + y \cdot y + z \cdot z} $

Parameters
xthe x-coordinate of the vector
ythe y-coordinate of the vector
zthe z-coordinate of the vector